Skip to main content

Unveiling Hidden Neural Codes: SIMPL – A Scalable and Fast Approach for Optimizing Latent Variables and Tuning Curves in Neural Population Data

Dr. Rishabh Pathak
This research paper presents SIMPL (Scalable Iterative Maximization of Population-coded Latents), a novel, computationally efficient algorithm designed to refine the estimation of latent variables and tuning curves from neural population activity. Latent variables in neural data represent essential low-dimensional quantities encoding behavioral or cognitive states, which neuroscientists seek to identify to understand brain computations better. Background and Motivation Traditional approaches commonly assume the observed behavioral variable as the latent neural code. However, this assumption can lead to inaccuracies because neural activity sometimes encodes internal cognitive states differing subtly from observable behavior (e.g., anticipation, mental simulation). Existing latent variable models face challenges such as high computational cost, poor scalability to large datasets, limited expressiveness of tuning models, or difficulties interpreting complex neural network-based functio...
Post a Comment

Continuous Theta Burst Stimulation (cTBS)

Image
Dr. Rishabh Pathak

Continuous Theta Burst Stimulation (cTBS) is a specific protocol of repetitive transcranial magnetic stimulation (rTMS) that is used to modulate cortical excitability and induce neuroplastic changes in the brain. Here is a detailed explanation of Continuous Theta Burst Stimulation:


1.      Definition:

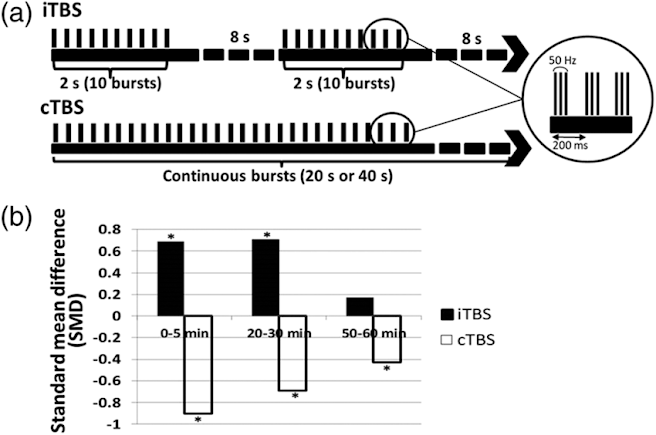
o   cTBS: Continuous Theta Burst Stimulation is a patterned form of rTMS that involves delivering bursts of magnetic pulses at a specific frequency and intensity over a continuous period of time to a targeted area of the brain. It is characterized by the application of theta-burst patterns of stimulation.

2.     Stimulation Parameters:

o   Theta Burst Pattern: The theta burst pattern consists of bursts of three pulses at 50 Hz repeated at a theta frequency (5 Hz). This pattern is delivered continuously over a specified duration, typically ranging from several seconds to minutes, depending on the research or clinical protocol.

o   Intensity and Duration: The intensity of cTBS is usually set as a percentage of the individual's resting motor threshold, ensuring that the stimulation is tailored to the specific cortical excitability of the target area. The duration of cTBS can vary based on the desired effects and experimental design.

3.     Mechanism of Action:

o   Inhibitory Effect: cTBS is primarily known for its inhibitory effects on cortical excitability. By delivering continuous theta burst patterns, the stimulation leads to a reduction in neuronal firing rates and synaptic transmission in the targeted brain region.

o   Long-Lasting Effects: cTBS has been shown to induce long-lasting changes in cortical excitability, with inhibitory effects persisting beyond the stimulation period. This ability to modulate neural activity and induce plastic changes makes cTBS a valuable tool for studying brain function and potential therapeutic applications.

4.    Applications:

o   Research: cTBS is widely used in research settings to investigate the role of inhibitory mechanisms in cortical function, neural plasticity, and motor learning. Researchers utilize cTBS to study the effects of cortical inhibition on cognitive processes, motor control, and sensory functions.

o Therapeutic Potential: In clinical applications, cTBS is being explored as a potential treatment strategy for neurological and psychiatric disorders. By modulating cortical excitability and neural networks, cTBS may offer therapeutic benefits for conditions such as depression, chronic pain, stroke recovery, and movement disorders.

5.     Clinical Studies:

o  Depression: cTBS has shown promise as a non-invasive treatment for depression, particularly in individuals who are resistant to traditional therapies. By targeting specific brain regions implicated in mood regulation, cTBS may help alleviate depressive symptoms and improve overall well-being.

o  Neurorehabilitation: In the field of neurorehabilitation, cTBS is being investigated as a potential adjunct therapy to enhance motor recovery following stroke, traumatic brain injury, or other neurological conditions. By modulating cortical plasticity, cTBS may facilitate motor relearning and functional recovery.

In summary, Continuous Theta Burst Stimulation is a specialized form of rTMS that exerts inhibitory effects on cortical excitability and induces long-lasting changes in neural activity. With applications in research and clinical settings, cTBS offers insights into brain function, neuroplasticity, and potential therapeutic interventions for a range of neurological and psychiatric disorders.

 

Categories:

Comments

Post a Comment

Popular posts from this blog

Relation of Model Complexity to Dataset Size

Dr. Rishabh Pathak
Core Concept The relationship between model complexity and dataset size is fundamental in supervised learning, affecting how well a model can learn and generalize. Model complexity refers to the capacity or flexibility of the model to fit a wide variety of functions. Dataset size refers to the number and diversity of training samples available for learning. Key Points 1. Larger Datasets Allow for More Complex Models When your dataset contains more varied data points , you can afford to use more complex models without overfitting. More data points mean more information and variety, enabling the model to learn detailed patterns without fitting noise. Quote from the book: "Relation of Model Complexity to Dataset Size. It’s important to note that model complexity is intimately tied to the variation of inputs contained in your training dataset: the larger variety of data points your dataset contains, the more complex a model you can use without overfitting....
Post a Comment
Read more

EEG Amplification

Dr. Rishabh Pathak
EEG amplification, also known as gain or sensitivity, plays a crucial role in EEG recordings by determining the magnitude of electrical signals detected by the electrodes placed on the scalp. Here is a detailed explanation of EEG amplification: 1. Amplification Settings : EEG machines allow for adjustment of the amplification settings, typically measured in microvolts per millimeter (μV/mm). Common sensitivity settings range from 5 to 10 μV/mm, but a wider range of settings may be used depending on the specific requirements of the EEG recording. 2. High-Amplitude Activity : When high-amplitude signals are present in the EEG, such as during epileptiform discharges or artifacts, it may be necessary to compress the vertical display to visualize the full range of each channel within the available space. This compression helps prevent saturation of the signal and ensures that all amplitude levels are visible. 3. Vertical Compression : Increasing the sensitivity value (e.g., from 10 μV/mm to...
Post a Comment
Read more

Linear Models

Dr. Rishabh Pathak
1. What are Linear Models? Linear models are a class of models that make predictions using a linear function of the input features. The prediction is computed as a weighted sum of the input features plus a bias term. They have been extensively studied over more than a century and remain widely used due to their simplicity, interpretability, and effectiveness in many scenarios. 2. Mathematical Formulation For regression , the general form of a linear model's prediction is: y^ ​ = w0 ​ x0 ​ + w1 ​ x1 ​ + … + wp ​ xp ​ + b where; y^ ​ is the predicted output, xi ​ is the i-th input feature, wi ​ is the learned weight coefficient for feature xi ​ , b is the intercept (bias term), p is the number of features. In vector form: y^ ​ = wTx + b where w = ( w0 ​ , w1 ​ , ... , wp ​ ) and x = ( x0 ​ , x1 ​ , ... , xp ​ ) . 3. Interpretation and Intuition The prediction is a linear combination of features — each feature contributes prop...
Post a Comment
Read more

Different Methods for recoding the Brain Signals of the Brain?

Dr. Rishabh Pathak
The various methods for recording brain signals in detail, focusing on both non-invasive and invasive techniques.  1. Electroencephalography (EEG) Type : Non-invasive Description : EEG involves placing electrodes on the scalp to capture electrical activity generated by neurons. It records voltage fluctuations resulting from ionic current flows within the neurons of the brain. This method provides high temporal resolution (millisecond scale), allowing for the monitoring of rapid changes in brain activity. Advantages : Relatively low cost and easy to set up. Portable, making it suitable for various applications, including clinical and research settings. Disadvantages : Lacks spatial resolution; it cannot precisely locate where the brain activity originates, often leading to ambiguous results. Signals may be contaminated by artifacts like muscle activity and electrical noise. Developments : ...
Post a Comment
Read more

Uncertainty Estimates from Classifiers

Dr. Rishabh Pathak
1. Overview of Uncertainty Estimates Many classifiers do more than just output a predicted class label; they also provide a measure of confidence or uncertainty in their predictions. These uncertainty estimates help understand how sure the model is about its decision , which is crucial in real-world applications where different types of errors have different consequences (e.g., medical diagnosis). 2. Why Uncertainty Matters Predictions are often thresholded to produce class labels, but this process discards the underlying probability or decision value. Knowing how confident a classifier is can: Improve decision-making by allowing deferral in uncertain cases. Aid in calibrating models. Help in evaluating the risk associated with predictions. Example: In medical testing, a false negative (missing a disease) can be worse than a false positive (extra test). 3. Methods to Obtain Uncertainty from Classifiers 3.1 ...
Post a Comment
Read more